Demystifying Naive Bayes in Machine Learning

1. Introduction to Naive Bayes: The Probabilistic Powerhouse

Naive Bayes is a fundamental yet powerful algorithm in the realm of machine learning, particularly in the domain of classification tasks. This probabilistic approach has stood the test of time, remaining relevant and effective even in the era of deep learning and complex neural networks. At its core, Naive Bayes leverages Bayes’ theorem, a principle of probability theory, to make predictions based on the likelihood of certain features occurring in different classes.

To truly appreciate the elegance of Naive Bayes, let’s dive into a real-world scenario. Imagine you’re a doctor trying to diagnose whether a patient has the flu. You observe symptoms like fever, cough, and fatigue. Naive Bayes would approach this problem by asking: “Given these symptoms, what’s the probability that the patient has the flu?” It would then compare this probability to the likelihood of other possible diagnoses, ultimately making a prediction based on the highest probability.

What sets Naive Bayes apart is its “naive” assumption of feature independence. In our flu example, it assumes that the presence of a fever doesn’t influence the likelihood of a cough, and vice versa. While this assumption rarely holds true in reality, it simplifies calculations and, surprisingly, often leads to accurate results.

The algorithm’s simplicity, coupled with its effectiveness, makes it a go-to choice for various applications, from spam email detection to sentiment analysis in natural language processing. As we delve deeper into the intricacies of Naive Bayes, we’ll uncover its mathematical foundations, explore its variants, and understand why it continues to be a staple in the machine learning toolkit.

2. The Mathematical Foundation: Bayes’ Theorem Unveiled

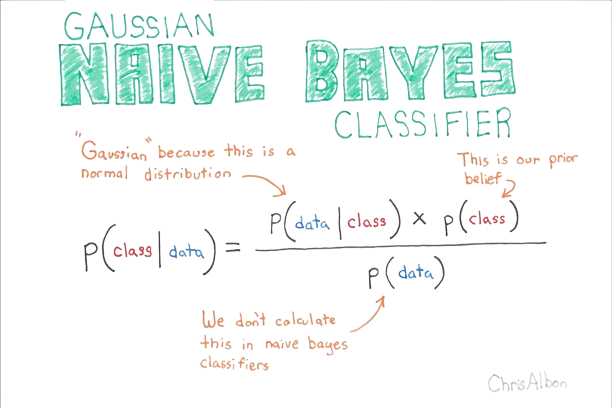
At the heart of Naive Bayes lies Bayes’ theorem, a fundamental principle in probability theory. To truly grasp the power of Naive Bayes, we must first understand this theorem and its application in machine learning contexts.

Bayes’ theorem is expressed mathematically as:

P(A|B) = (P(B|A) * P(A)) / P(B)

Where:

• P(A|B) is the probability of event A occurring given that B has occurred
• P(B|A) is the probability of event B occurring given that A has occurred
• P(A) is the probability of event A occurring
• P(B) is the probability of event B occurring

In the context of Naive Bayes classification, we can rewrite this as:

P(class|features) = (P(features|class) * P(class)) / P(features)

Let’s break this down with a concrete example. Suppose we’re building a spam email classifier. Our classes are “spam” and “not spam”, and our features might include words like “viagra”, “free”, and “million dollars”.

P(spam|”free” appears) = (P(“free” appears|spam) * P(spam)) / P(“free” appears)

To calculate this, we would need:

1. The probability of “free” appearing in spam emails
2. The overall probability of an email being spam
3. The overall probability of “free” appearing in any email

The “naive” part comes into play when we consider multiple features. Naive Bayes assumes that these features are independent of each other. So, if we’re looking at both “free” and “viagra”, we calculate:

P(spam|”free” AND “viagra”) = P(spam) * P(“free”|spam) * P(“viagra”|spam) / (P(“free”) * P(“viagra”))

This assumption of independence, while often unrealistic, simplifies calculations and allows Naive Bayes to scale efficiently to high-dimensional datasets.

To illustrate the power of this approach, let’s consider a small dataset:

Email	Contains “free”	Contains “viagra”	Class
1	Yes	No	Spam
2	No	Yes	Spam
3	Yes	Yes	Spam
4	No	No	Not Spam
5	Yes	No	Not Spam

From this data, we can calculate:

• P(spam) = 3/5
• P(“free”|spam) = 2/3
• P(“viagra”|spam) = 2/3
• P(“free”) = 3/5
• P(“viagra”) = 2/5

Now, if we receive a new email containing both “free” and “viagra”, we can calculate:

P(spam|”free” AND “viagra”) ∝ (3/5) * (2/3) * (2/3) = 4/15

P(not spam|”free” AND “viagra”) ∝ (2/5) * (1/2) * (0/2) = 0

The ∝ symbol means “proportional to”, as we’ve omitted the denominator (which is constant for both calculations). Since 4/15 > 0, we would classify this email as spam.

This simplified example demonstrates the essence of how Naive Bayes makes decisions based on probabilities derived from observed data. In practice, we often use logarithms to avoid underflow with very small probabilities, and we may apply smoothing techniques to handle cases where we have zero probabilities.

Understanding this mathematical foundation is crucial for implementing Naive Bayes effectively and interpreting its results. As we progress through this blog, we’ll explore how this theory translates into practical applications and different variants of the algorithm.

3. Variants of Naive Bayes: Tailoring the Algorithm to Your Data

While the core concept of Naive Bayes remains consistent, several variants have been developed to better handle different types of data and distributions. Each variant has its strengths and is suited to specific types of problems. Let’s explore the three main variants of Naive Bayes and understand when to use each one.

3.1 Gaussian Naive Bayes

Gaussian Naive Bayes assumes that the continuous values associated with each class are distributed according to a Gaussian (normal) distribution. This variant is particularly useful when dealing with continuous data, such as measurements or sensor readings.

Key characteristics:

• Assumes features follow a normal distribution
• Calculates mean and standard deviation for each class
• Suitable for continuous data

Real-world example: Imagine you’re developing a system to classify fruits based on their weight and diameter. The weight and diameter of apples, oranges, and bananas might each follow a Gaussian distribution. Gaussian Naive Bayes would be an excellent choice for this scenario.

Python implementation snippet:

python

from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# Load the Iris dataset
iris = load_iris()
X, y = iris.data, iris.target

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Create and train the model
gnb = GaussianNB()
gnb.fit(X_train, y_train)

# Make predictions
y_pred = gnb.predict(X_test)

# Calculate accuracy
accuracy = (y_pred == y_test).sum() / len(y_test)
print(f"Accuracy: {accuracy:.2f}")

3.2 Multinomial Naive Bayes

Multinomial Naive Bayes is typically used for discrete data, particularly in document classification problems where we’re dealing with word counts or frequencies.

Key characteristics:

• Assumes features are generated from a multinomial distribution
• Often used with text classification
• Requires integer feature counts (or fractional counts for fractional samples)

Real-world example: In sentiment analysis of movie reviews, where each word’s frequency in the review is a feature, Multinomial Naive Bayes would be an excellent choice. It can effectively capture the relationship between word frequencies and sentiment classes.

Python implementation snippet:

python

from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split

# Sample data
texts = ["I love this movie", "This movie is terrible", "Great acting", "Poor plot", "Awesome film"]
labels = [1, 0, 1, 0, 1]  # 1 for positive, 0 for negative

# Vectorize the text
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(texts)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.3, random_state=42)

# Create and train the model
mnb = MultinomialNB()
mnb.fit(X_train, y_train)

# Make predictions
y_pred = mnb.predict(X_test)

# Calculate accuracy
accuracy = (y_pred == y_test).sum() / len(y_test)
print(f"Accuracy: {accuracy:.2f}")

3.3 Bernoulli Naive Bayes

Bernoulli Naive Bayes is designed for binary/boolean features. It’s particularly useful in text classification tasks where we care about whether a word appears in a document, rather than its frequency.

Key characteristics:

• Assumes features are binary (0 or 1)
• Penalizes the non-occurrence of a feature that’s indicative of a class
• Suitable for short texts or when presence/absence is more important than frequency

Real-world example: In spam detection, where the presence or absence of certain words is more important than their frequency, Bernoulli Naive Bayes would be an excellent choice. It can effectively capture whether suspicious words appear in an email, regardless of how many times they appear.

Python implementation snippet:

python

from sklearn.naive_bayes import BernoulliNB
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split

# Sample data
texts = ["Free offer", "Meeting schedule", "Win a prize", "Project update", "Claim your reward"]
labels = [1, 0, 1, 0, 1]  # 1 for spam, 0 for not spam

# Vectorize the text (binary)
vectorizer = CountVectorizer(binary=True)
X = vectorizer.fit_transform(texts)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.3, random_state=42)

# Create and train the model
bnb = BernoulliNB()
bnb.fit(X_train, y_train)

# Make predictions
y_pred = bnb.predict(X_test)

# Calculate accuracy
accuracy = (y_pred == y_test).sum() / len(y_test)
print(f"Accuracy: {accuracy:.2f}")

Choosing the right variant of Naive Bayes depends on your data and problem context. Gaussian Naive Bayes works well with continuous data, Multinomial Naive Bayes excels in text classification with word frequencies, and Bernoulli Naive Bayes is ideal for binary features or short texts.

By understanding these variants and their applications, you can leverage the full power of Naive Bayes across a wide range of machine learning tasks. In the next section, we’ll explore the advantages and limitations of Naive Bayes, helping you make informed decisions about when to use this algorithm in your projects.

4. Advantages and Limitations: When to Choose Naive Bayes

Naive Bayes has carved out a significant niche in the machine learning landscape due to its unique characteristics. However, like any algorithm, it comes with its own set of strengths and weaknesses. Understanding these can help you make informed decisions about when to employ Naive Bayes in your projects and when to consider alternative approaches.

Advantages:

1. Simplicity and Efficiency:
   Naive Bayes is incredibly simple to implement and computationally efficient. It can be trained quickly even on large datasets, making it an excellent choice for real-time prediction scenarios or when working with limited computational resources. Example: In a startup environment where quick prototyping is crucial, Naive Bayes can be rapidly deployed for tasks like customer churn prediction, allowing for fast iteration and testing of different feature sets.
2. Performance with Small Datasets:
   Naive Bayes can perform surprisingly well with small training datasets. It doesn’t require as much training data as some more complex algorithms to achieve reasonable performance. Example: In medical diagnosis for rare diseases where data is scarce, Naive Bayes can still provide valuable insights based on limited patient records.
3. Handling Multiple Classes:
   Naive Bayes naturally extends to multi-class classification problems, making it versatile for various applications. Example: In document classification where texts need to be categorized into multiple topics (e.g., sports, politics, technology, entertainment), Naive Bayes can efficiently handle this multi-class scenario.
4. Resistant to Irrelevant Features:
   Naive Bayes is less affected by irrelevant features compared to some other algorithms. It can often maintain good performance even when some features are not particularly informative. Example: In email spam detection, even if certain words are included that aren’t typically indicative of spam, Naive Bayes can still make accurate classifications based on other relevant features.
5. Works Well with High-Dimensional Data:
   Naive Bayes is particularly effective with high-dimensional data, such as text classification problems where each word is treated as a feature. Example: In sentiment analysis of product reviews, where the vocabulary (feature set) can be extensive, Naive Bayes can efficiently process and classify based on this high-dimensional input.

Limitations:

1. Independence Assumption:
   The “naive” assumption of feature independence is often unrealistic and can lead to suboptimal performance when strong feature correlations exist. Example: In image classification, pixel values are often highly correlated with their neighboring pixels, violating the independence assumption of Naive Bayes.
2. Zero Frequency Problem:
   When a categorical variable has a category in the test data that was not observed in the training data, the model will assign a zero probability and be unable to make a prediction. This is known as the “zero frequency” problem. Example: In a movie genre classification task, if a new genre appears in the test set that wasn’t in the training data, Naive Bayes would fail to classify it correctly.
3. Estimating Probabilities:
   Naive Bayes can be sensitive to how probabilities are estimated from the training data, especially with small datasets. Example: In a credit scoring application with limited historical data, the estimated probabilities might not accurately reflect the true underlying distribution, leading to biased predictions.
4. Inability to Learn Interactions:
   Due to the independence assumption, Naive Bayes cannot learn interactions between features. Example: In predicting housing prices, the interaction between the number of bedrooms and the total square footage is important, but Naive Bayes would treat these features independently.
5. Continuous Data Challenges:
   While Gaussian Naive Bayes can handle continuous data, it assumes a normal distribution, which may not always be the case in real-world scenarios. Example: In financial modeling, stock returns often follow non-normal distributions, which could lead to inaccurate predictions if using Gaussian Naive Bayes.

To illustrate these points, let’s consider a comparison table of Naive Bayes with other common algorithms:

Aspect	Naive Bayes	Logistic Regression	Decision Trees	Support Vector Machines
Speed of Training	Very Fast	Fast	Moderate	Slow for large datasets
Interpretability	High	Moderate	High	Low
Handling of High-Dimensional Data	Excellent	Good	Poor	Excellent
Ability to Capture Feature Interactions	Poor	Moderate	Excellent	Good
Performance with Small Datasets	Good	Moderate	Poor	Moderate
Resistance to Overfitting	High	Moderate	Low (without pruning)	Moderate

In conclusion, Naive Bayes shines in scenarios where quick training, high-dimensional data, and multi-class problems are involved. It’s particularly well-suited for text classification tasks, spam detection, and sentiment analysis. However, for problems where feature interactions are crucial or when dealing with strongly correlated features, other algorithms might be more appropriate.

Understanding these advantages and limitations allows you to make informed decisions about when to employ Naive Bayes in your machine learning projects. In the next section, we’ll explore real-world applications of Naive Bayes, showcasing its versatility across various domains.

5. Real-World Applications: Naive Bayes in Action

Naive Bayes, despite its simplicity, finds applications in numerous real-world scenarios. Its efficiency, ability to handle high-dimensional data, and effectiveness in certain types of problems make it a go-to algorithm for many practitioners. Let’s explore some of the most impactful and interesting applications of Naive Bayes across various domains.

5.1. Email Spam Detection:

One of the most well-known applications of Naive Bayes is in email spam filtering. The algorithm analyzes the content and metadata of emails to classify them as spam or not spam.

Example implementation:

python

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split

# Sample data
emails = [
    "Get rich quick! Buy now!",
    "Meeting at 3 PM tomorrow",
    "Claim your prize now!",
    "Project report due next week",
    "Unlimited offer! Don't miss out!"
]
labels = [1, 0, 1, 0, 1]  # 1 for spam, 0 for not spam

# Vectorize the text
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(emails)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.3, random_state=42)

# Train the model
spam_classifier = MultinomialNB()
spam_classifier.fit(X_train, y_train)

# Test the model
accuracy = spam_classifier.score(X_test, y_test)
print(f"Spam detection accuracy: {accuracy:.2f}")

# Classify a new email
new_email = ["Free webinar on data science"]
new_email_vectorized = vectorizer.transform(new_email)
prediction = spam_classifier.predict(new_email_vectorized)
print(f"New email classified as: {'Spam' if prediction[0] == 1 else 'Not Spam'}")

5.2. Sentiment Analysis:

Naive Bayes is widely used in sentiment analysis tasks, such as determining whether a product review is positive or negative.

Example:

python

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split

# Sample data
reviews = [
    "This product is amazing! I love it.",
    "Terrible experience, would not recommend.",
    "Great value for money, very satisfied.",
    "Disappointing quality, not worth the price.",
    "Exceeded my expectations, fantastic purchase!"
]
sentiments = [1, 0, 1, 0, 1]  # 1 for positive, 0 for negative

# Vectorize the text
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(reviews)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, sentiments, test_size=0.3, random_state=42)

# Train the model
sentiment_classifier = MultinomialNB()
sentiment_classifier.fit(X_train, y_train)

# Test the model
accuracy = sentiment_classifier.score(X_test, y_test)
print(f"Sentiment analysis accuracy: {accuracy:.2f}")

# Analyze a new review
new_review = ["The product is okay, but could be better"]
new_review_vectorized = vectorizer.transform(new_review)
prediction = sentiment_classifier.predict(new_review_vectorized)
print(f"New review sentiment: {'Positive' if prediction[0] == 1 else 'Negative'}")

5.3. Medical Diagnosis:

Naive Bayes can be used to assist in medical diagnosis by predicting the likelihood of a disease based on symptoms.

Example:

python

from sklearn.naive_bayes import GaussianNB
import numpy as np

# Sample data: [fever, cough, fatigue]
symptoms = np.array([
    [101, 1, 1],
    [99, 0, 0],
    [102, 1, 1],
    [98, 0, 1],
    [100, 1, 0]
])
diagnoses = np.array([1, 0, 1, 0, 1])  # 1 for flu, 0 for no flu

# Train the model
diagnosis_model = GaussianNB()
diagnosis_model.fit(symptoms, diagnoses)

# Diagnose a new patient
new_patient = np.array([[100.5, 1, 1]])
prediction = diagnosis_model.predict(new_patient)
probability = diagnosis_model.predict_proba(new_patient)

print(f"Diagnosis: {'Flu' if prediction[0] == 1 else 'No Flu'}")
print(f"Probability of flu: {probability[0][1]:.2f}")

5.4. Document Classification:

Naive Bayes is effective in categorizing documents into predefined topics or genre

Example:

python

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split

# Sample data
documents = [
    "The latest smartphone features a powerful camera",
    "New study reveals insights into climate change",
    "Stock market reaches record high amid economic growth",
    "Scientists discover new species in the Amazon rainforest",
    "Tech company launches innovative AI-powered assistant"
]
categories = [0, 1, 2, 1, 0]  # 0: Technology, 1: Science, 2: Finance

# Vectorize the text
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(documents)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, categories, test_size=0.3, random_state=42)

# Train the model
doc_classifier = MultinomialNB()
doc_classifier.fit(X_train, y_train)

# Test the model
accuracy = doc_classifier.score(X_test, y_test)
print(f"Document classification accuracy: {accuracy:.2f}")

# Classify a new document
new_doc = ["Researchers develop new renewable energy technology"]
new_doc_vectorized = vectorizer.transform(new_doc)
prediction = doc_classifier.predict(new_doc_vectorized)
category_map = {0: "Technology", 1: "Science", 2: "Finance"}
print(f"New document classified as: {category_map[prediction[0]]}")

5.5. Recommender Systems:

Naive Bayes can be used in collaborative filtering for recommender systems, predicting user preferences based on past behavior.

Example:

python

from sklearn.naive_bayes import MultinomialNB
import numpy as np

# Sample data: User ratings for movies (0: not rated, 1-5: rating)
user_ratings = np.array([
    [5, 4, 0, 2, 1],
    [3, 0, 4, 0, 2],
    [4, 3, 0, 5, 0],
    [0, 2, 4, 0, 3],
    [5, 0, 0, 3, 2]
])

# Train a model for each movie
movie_models = []
for movie in range(user_ratings.shape[1]):
    model = MultinomialNB()
    X = user_ratings[:, :movie].copy()
    X = np.hstack((X, user_ratings[:, movie+1:]))
    y = user_ratings[:, movie]
    model.fit(X, y)
    movie_models.append(model)

# Predict rating for a new user
new_user = np.array([4, 0, 3, 0, 2])
for movie in range(len(movie_models)):
    if new_user[movie] == 0:
        X = new_user.copy()
        X = np.delete(X, movie)
        prediction = movie_models[movie].predict([X])
        print(f"Predicted rating for movie {movie+1}: {prediction[0]}")

These examples demonstrate the versatility of Naive Bayes across different domains. From text classification tasks like spam detection and sentiment analysis to more complex applications in medical diagnosis and recommender systems, Naive Bayes proves to be a valuable tool in a data scientist’s toolkit.

Its simplicity, efficiency, and effectiveness in handling high-dimensional data make it particularly well-suited for these types of problems. However, it’s important to remember the limitations discussed earlier, such as the assumption of feature independence, which may not always hold true in real-world scenarios.

As with any machine learning technique, the key to success lies in understanding the problem domain, carefully preparing and preprocessing the data, and critically evaluating the model’s performance. Naive Bayes, when applied appropriately, can provide quick and reliable results for a wide range of classification tasks.

6. Conclusion: The Enduring Relevance of Naive Bayes in Machine Learning

As we conclude our deep dive into Naive Bayes, it’s clear that this algorithm, despite its simplicity and “naive” assumptions, continues to be a powerful and relevant tool in the modern machine learning landscape. Let’s recap the key points we’ve covered and reflect on the role of Naive Bayes in today’s data-driven world.

1. Simplicity Meets Effectiveness:
   Naive Bayes stands out for its elegant simplicity. Based on Bayes’ theorem and the assumption of feature independence, it provides a straightforward yet often surprisingly effective approach to classification tasks. This simplicity translates to computational efficiency, making Naive Bayes an excellent choice for large-scale applications and real-time predictions.
2. Versatility Across Domains:
   From text classification and spam detection to medical diagnosis and recommender systems, Naive Bayes has proven its versatility across a wide range of applications. Its ability to handle high-dimensional data makes it particularly well-suited for tasks involving text analysis and natural language processing.
3. Performance with Limited Data:
   In scenarios where training data is scarce, Naive Bayes often outperforms more complex algorithms. This characteristic makes it valuable in domains where data collection is challenging or expensive, such as in certain medical or scientific research contexts.
4. Probabilistic Foundation:
   The probabilistic nature of Naive Bayes provides not just classifications but also probabilities associated with those classifications. This can be crucial in decision-making processes where understanding the confidence of predictions is important.
5. Interpretability:
   In an era where model interpretability is increasingly important, Naive Bayes offers clear insights into how it arrives at its predictions. The probabilities associated with each feature can be easily examined, providing transparency that is often lacking in more complex “black box” models.
6. Limitations and Considerations:
   While powerful, Naive Bayes is not without its limitations. The assumption of feature independence, while simplifying calculations, can lead to suboptimal performance in scenarios where features are strongly correlated. Additionally, the algorithm can be sensitive to input data characteristics and may require careful feature engineering and selection.
7. Complementary Role in Modern ML Ecosystems:
   In today’s machine learning landscape, Naive Bayes often serves as a baseline model or as part of an ensemble of algorithms. Its quick training time and good out-of-the-box performance make it an excellent starting point for many classification tasks, providing a benchmark against which more complex models can be compared.
8. Ongoing Research and Development:
   The machine learning community continues to explore ways to enhance and extend Naive Bayes. Techniques like feature selection, smoothing methods, and hybrid approaches that combine Naive Bayes with other algorithms are areas of ongoing research, aiming to address some of its limitations while preserving its core strengths.

In conclusion, Naive Bayes remains a vital component of the machine learning toolkit. Its blend of simplicity, efficiency, and effectiveness makes it a valuable asset for data scientists and machine learning practitioners. Whether used as a standalone classifier, a baseline model, or part of a more complex ensemble, Naive Bayes continues to contribute significantly to solving real-world problems across diverse domains.

As we look to the future, it’s clear that while more complex algorithms like deep neural networks may dominate headlines, the fundamental principles embodied by Naive Bayes – probabilistic reasoning, computational efficiency, and interpretability – will continue to play a crucial role in advancing the field of machine learning.

For aspiring data scientists and seasoned practitioners alike, a deep understanding of Naive Bayes provides not just practical skills but also insights into the core principles of probabilistic machine learning. As you continue your journey in this exciting field, remember that sometimes, the most powerful solutions can come from the simplest of ideas – a truth that Naive Bayes exemplifies beautifully.